Concept of Game Theory and Saddle Points
“Nothing’s ever for sure, that’s the only sure thing I know”
-Nash (A Beautiful Mind)
Game Theory is the study of the ways in which interacting choices of economic agents produce outcomes with respect to the preferences of the participating agents, where the outcomes in question is unbiased and irrespective of one’s choices. It is a branch of applied mathematics that provide the necessary tools for analyzing situations in which the participants i.e the “players” make decisions that are interdependent. This interdependence cause each player to consider other player’s possible decisions or strategies, in formulating strategy. A solution to a game describes the optimal decisions of the players, who may have simple, opposed or mixed interests and the outcomes come as a result to such decisions.
In fact , Game Theory was originally developed by the Hungarian-born American mathematician John von Neumann and his colleague Oskar Morgenstern ,a German-born American economist, to solve problems in economics in around 1928. His 1928 paper written in German, established John Neumann as the “Father of Game Theory”. It was later developed by an American mathematical scientist George Bernard Dantzig.
For better understanding of the concept we need to know about the tools of Game Theory.
· PLAYERS: Players are basically the participants involved in a game.
· STRATEGY : Strategy is the course of action taken by the players
· PURE STRATEGY: Pure Strategy is a decision making rule in which one particular course of action is selected.
· MIXED STRATEGY: Mixed Strategy is a decision making rule in which the player decides in advance, to choose his courses of action with some definite probability distribution.
· OPTIMUM STRATEGY: A course of action which puts the player in the most preferred position.
· FAIR GAME: if the value of the game is zero, it’s called a fair game.
· When only two people are involved in a game and if the gain made by a player is equal to the loss made by the other player, it is called a ZERO SUM GAME. It is called a ‘two person zero-sum game’ sometimes and even called ‘rectangular game’ sometimes owing to the rectangular form of the payoff matrix.
SADDLE POINT ,in mathematics, is a point on the surface of the graph of a function where the slopes (derivatives) in orthogonal directions are all zero (a critical point), but which is not a local extremum of the function. It’s also called the minimax point i.e if the max-min value equals to the min-max value of the game, the the game is said to have a Saddle Point and the corresponding strategy is called Optimum Strategy.
Theorem to prove the Existence of Saddle Point
Let f(x,y) be a real valued function of x and y such that f(x,y) is a real number for x⋲A and y⋲B , A and B being two sets. Further if both max x⋲A min y⋲Bf(x,y) and min y⋲B max x⋲A f(x,y) exist then max x⋲A min y⋲Bf(x,y) <=min y⋲B max x⋲A f(x,y)
Let us consider a playoff matrix given by
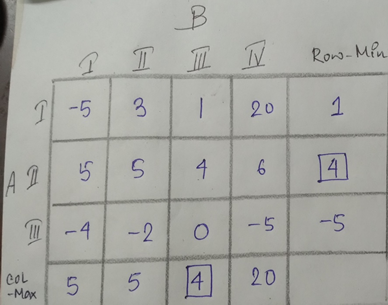
Let A be the maximizing player and B be the minimizing player.
Here the min-max=max-min
= 4.
Then this position is the saddle
point of the payoff matrix
and the pure strategies II for A
and III for B are the optimal solution of the game, which is written as (II ,III). Thus 4 ,the saddle point, is the value of the game.
Here max-min= Max{1, 4, -5} = 4 and min-max= Min{5,5,4,20}=4. Hence the game is strictly determinable.
Game Theory is a classic theory which holds a special significance in formulating the alternative strategy to compete with one another and in the same sense it is a essential tool for decision making process according to fluctuations in relevant contents.
Even if unaware, Game Theory is often present in real estate negotiations which makes the game bit more clear than in other situations.
Author’s Note: I have just outlined the concept of Game Theory in this story. If you want the discussion of some specific concept do comment below!!
Till then TAKE CARE!
References: Ghosh & Chakroborty.
